Comparison of 99m Tc DTPA vs Five Methods to Estimate Glomerular Filtration Rate in Children with Renal Transplantation

Barbara Ulibarri; Carlos Martinez-Duncker; Claudia Camarillo; Enrique Omar Guadarrama; Pilar Garcia Roca; Ricardo Munoz Arizpe; Mara Medeiros

doi:https://

Barbara Ulibarri¹, Carlos Martinez-Duncker², Claudia Camarillo², Enrique Omar Guadarrama¹, Pilar Garcia Roca³, Ricardo Munoz Arizpe³, Mara Medeiros³.

¹Departamento de Nefrologia, Hospital Infantil de Mexico Federico Gomez, Mexico,
²Departamento Medicina Nuclear, Hospital Infantil de Mexico Federico Gomez, Mexico,
³Laboratorio de Investigacion en Nefrologia., Hospital Infantil de Mexico Federico Gomez, Mexico.

ADDRESS FOR CORRESPONDENCE
Mara Medeiros, Laboratorio de Investigacion en Nefrologia, Hospital Infantil de Mexico Federico Gomez, Dr. Marquez 162 Col. Doctores., Mexico D.F., Mexico 06720.
Email: maramedeiros@hotmail.com

Show affiliations

Abstract

The purpose of the study was to compare the GFR obtained with ^99mTc DTPA against five other methods: the GFR measured by 24 hours creatinine clearance (Ccr), and four creatinine-based equations (Schwartz, Counahan-Barrat, Morris and Leger). A descriptive, cross-sectional study was performed in 42 renal transplant children; a 24 hours urine collection was obtained for creatinine clearance. A ^99mTc-DTPA renal gammagram was performed the same day. The mean GFR (mL/min1.73m2BSA) obtained with 99mTc-DTPA was 66.9 ± 15, whereas by Ccr was 68.7 ± 24.4, by Schwartz formula 81.8 ± 16, by the Counahan-Barrat equation was 57.6 ± 13.6, by Morris equation 60.7 ± 14.5 and by Leger equation 73.2 ± 18. The predictive performance was evaluated calculating bias as mean prediction error (MPE) and precision (Mean Squared Error, MSE). The Schwartz formula had a MPE of 14.8 and MSE of 9223. The Ccr had a MPE of 1.7 and MSE of 132, Counahan-Barrat MPE -9.4, MSE 3727, Morris -6.28, MSE 1656, Leger -6.2 MSE 2000. Ccr had the lowest bias but is not precise to estimate GFR in renal transplant children. The Morris equation had better predictive performance in renal transplant children than the Schwartz, Counahan-Barrat and Leger equations.

Keywords

Glomerular filtration rate, renal transplant, children, Schwartz, GFR measurement

Introduction

According to the NKF-K/DOQI guidelines to evaluation, classification and stratification of chronic kidney disease in children and adolescents, the estimates of glomerular filtration rate (GFR) are the best indices of the level of kidney function, and the creatinine clearance using timed urine collections do not improve the estimated GFR over that provided by prediction equations [1]. The GFR estimation in children is made by exogenous markers such as inulin, cystatine C, iothalamate or the radiolabeled ^99mTecnetium diethylenetriamine pentaacetic acid (^99mTc-DTPA), accepted as the best methods. Nevertheless, these procedures are invasive, time-consuming and expensive, and not easy to perform in the every day practice [2]. For these reasons children are more frequently monitored with the GFR prediction equations using serum-creatinine based formulas. The GFR prediction equations are more accurate when GFR is normal (>90mL/min per 1.73 m²), otherwise they tend to overestimate the GFR [3]. The majority of the equations used have been initially developed for native kidneys, but a caveat appears when the equation are used to estimate the GFR in transplanted kidneys, since the nephron mass of the graft is never taken into account [4]. There are several studies in adults comparing equations to estimate GFR in renal transplant recipients. In general the equation proposed by the Modification of Diet in Renal Diseases Study, also known as MDRD formula has shown better predictive performance than the Cockcroft-Gault or the Nankivell equations [5-7], but it underestimate the number of patients with declining function [8]. These formulas are not recommended for children.

Methods & Materials

Patients with renal transplant and stable renal function (defined as those in whom the serum creatinine levels had not changed by more than 0.2 mg per deciliter during the previous three months) were invited to participate in the study. Those patients with graft dysfunction or known recurrence of the original disease were excluded. The study was approved by the IRB, and parental and children informed consent/assent was obtained in all cases. The gold standard used for estimate GFR was ^99m Tc-DTPA, since it has a clearance similar to inulin [9]. All studies were performed according the Guidelines for Nuclear Medicine of the Health Laws in our country. Dynamic images were obtained in supine position after an intravenous administration of ^99m Tc-DTPA dose, using a gamma camera during 30 minutes and then processed to generate the time-activity curves that allow to analyze the perfusion and filtration. A Gamma camera Siemens MultiSPECTII was used. Renograms were obtained and processed with a commercial nuclear medicine software (Siemens ICON). Serum and urine creatinine were measured by the kinetic Jaffe method using the Synchron CX3 automated analyzer.

24h Creatinine clearance (Ccr) was obtained with the formula:

Ccr = Ucr V/Scr ,
where: Ucr : urine creatinine concentration, V: flow rate of urine in millilitres per minute and Scr : serum creatinine. The creatinine clearance is normalized to body surface area x 1.73 m².

GFR was also estimated (eGFR) by the following equations:

1) Schwartz formula:

eGFR (ml/min/1.73 m²)= kL/ Scr (mg/dL), where:

L : length in centimeters, Scr : serum creatinine, k : constant value of 0.55 for children and adolescent girls, and 0.7 for adolescent boys [10-12].

2) Counahan-Barrat Formula [13]:

eGFR = 0.43 x Height (cm)/ Scr (mg/dL)

3) Morris equation [14]:
eGFR= 40 x height (cm) / Scr (μmol/L)

4) Leger formula [15]:

eGFR= 56.7 x body weight (kg) + 0.142 x Height (cm)2/ Scr (μmol/L)

The GFR value was corrected to body surface area x 1.73 m²

Statistical Analysis

We used the GraphPad Prism version 5.0 for Mac (GraphPad software, San Diego, CA) for data analysis. The GFR obtained by Ccr and the four equations were compared to ^99mTc-DTPA by paired t test and Pearson correlation. Agreement between methods was tested by the Bland and Altman plot method, the difference between the two measurements is plotted as a function of the average of the two measurements of each sample. It also provides the standard deviation of the differences between the two assay methods to calculate the limits of agreement, computed as the mean bias 1.96 times its standard deviation. The predictive performance of the different methods to assess GFR were analyzed by measuring bias and precision according to the formula suggested by Sheiner and Beal [16].

-Bias (Mean prediction Error) as: MPE = Σ(PRED-OBS)/n where PRED is the predicted value, OBS is the GFR observed by ^99mTc-DTPA, and n is the number of observations. An unbiased prediction results in a MPE value of zero. A negative MPE value indicates underestimation by the predictor and a positive MPE indicates overestimation. The precision of the predictions was estimated as Mean squared error (MSE) as: MSE= Σ(PRED-OBS)2/n. The ideal prediction yields a MSE of zero, were PRED=OBS. A high MSE value indicates poor predictive performance.

Results

A total of 42 patients were included in the study. Demographic data is depicted in Table 1. The values of GFR (mL/min/1.73m²BSA) by ^99mTc-DTPA and the eGFR by 24hCcr as well as the values for the four equations in each patient are shown in Table 2. The mean GFR obtained with ^99m Tc-DTPA was 66.9 mL/min ± 15, whereas by Ccr was 68.7 ± 24.4, by Schwartz formula 81.8 ± 15.9, by the Counahan-Barrat equation was 57.6 ± 13.6, by Morris equation 60.7 ± 14.5 and by Leger equation 73.2 ±18.3. GFR by all methods was normally distributed by D'Agostino & Pearson omnibus normality test. There was a significant correlation between GFR by ^99mTc-DTPA vs. Ccr (Pearson r = 0.316, p= 0.040), ^99mTc-DTPA vs. Schwartz (Pearson r = 0.500, p=0.0007), ^99mTc-DTPA vs. Counahan-Barrat formula ( r= 0.492, p=0.0009), ^99mTc-DTPA vs. Morris (r= 0.492, p=0.0009) and ^99mTc-DTPA vs. Leger (r= 0.494, p= 0.0009) (Figure 1). Nevertheless, when comparing by paired t test no difference was found between ^99mTc-DTPA vs. Ccr (p=0.64) but there was statistically significant difference between ^99mTc-DTPA and all the equations (Table 2).

Table 1. Patient's characteristics

Characteristic	Value
Age (years mean + SD)	14.7 + 2.5
Gender Male Female	24 18
Time post-renal transplant (months + SD)	26.17 + 6
Graft source Deceased donor Living donor	27 15
Immunosuppression regime PDN/MMF/Tac PDN/AZA/Tac PDN/MMF/CsA PDN/SRL/CsA PDN/MMF PDN/Tac PDN/CsA	28 (66.7%) 2 (4.8%) 1 (2.3%) 6 (14.2%) 2 (4.8%) 2 (4.8 %) 1 (2.3 %)
Acute rejection history n (%)	25 (59%)
Serum creatinine (mg/dL mean + SD)	1.18 + 0.3

PDN: prednisone, MMF: Mycophenolate mofetil, CsA: Cyclosporin, Tac: tacrolimus, SRL: sirolimus

Table 2. GFR in 42 renal transplant children

Patient	⁹⁹Tc-DTPA	Ccr	Schwartz	Counahan-Barrat	Morris	Leger
1.	53.1	59.68	93.30	57.00	60.61	81.32
2.	50.6	31.11	59.60	37.00	38.76	44.77
3.	75.2	78.22	83.46	51.00	54.20	66.25
4.	88.7	60.82	78.00	48.00	50.65	58.53
5.	74.7	82	91.90	72.00	76.01	87.57
6.	71.75	40.9	92.90	57.00	60.33	70.67
7.	75.7	93.58	99.10	61.00	64.39	76.60
8.	54.2	64.34	50.00	31.00	32.47	37.49
9.	56.7	101.90	100.30	78.00	82.95	96.98
10.	75	56.75	65.50	51.00	54.20	62.74
11.	63.6	57.52	81.50	50.00	52.92	64.35
12.	73.8	52.48	103.00	80.00	85.06	103.80
13.	75.5	121	103.90	63.00	66.94	77.60
14.	85	104.9	89.20	55.00	57.95	68.79
15.	50.3	48.81	67.94	42.00	44.12	52.23
16.	58.9	64.78	81.50	50.00	52.92	60.80
17.	59.4	49.2	57.30	45.00	47.08	54.94
18.	37.5	34.34	55.41	34.00	35.98	42.40
19.	50.6	26.94	72.40	45.00	47.06	56.31
20.	58.1	87.37	88.00	69.00	72.73	90.93
21.	64	46.49	78.00	48.00	47.88	55.29
22.	47.6	74.02	73.00	45.00	47.40	58.99
23.	63	105.18	101.00	79.00	83.52	98.69
24.	88.7	87.92	99.27	61.00	64.46	74.85
25.	46.6	66.18	67.37	53.00	55.68	66.34
26.	78.3	56.06	78.31	61.00	64.77	79.49
27.	56.7	71.21	98.46	60.00	63.94	75.43
28.	78.4	80.82	88.70	55.00	57.64	71.98
29.	101.2	41.76	114.70	90.00	94.81	111.89
30.	78.4	92.86	104.50	82.00	86.36	101.95
31.	76.6	43.25	66.00	51.00	54.20	60.46
32.	37.9	24.41	63.80	50.00	52.60	62.94
33.	66.2	50.50	68.29	53.00	56.44	68.71
34.	69.4	77.81	71.75	56.00	59.30	69.26
35.	78	65.57	68.50	54.00	56.64	66.06
36.	67.1	71.98	108.80	85.00	89.94	111.00
37.	62.2	116.84	76.00	62.00	63.13	81.51
38.	74.2	60.63	87.30	68.00	72.16	92.97
39.	102	92.28	88.00	69.00	72.73	99.83
40.	76.2	89.12	72.80	57.00	60.23	86.42
41.	55.3	54.90	74.00	58.00	60.98	71.80
42.	56.8	99.64	72.80	45.00	47.27	55.71
Mean	66.98	68.7	81.8	57.6	60.7	73.2
SD	15	24.4	15.9	13.6	14.5	18.3
Paired t test p value		0.64	<0.0001	0.0001	0.009	0.021

The Bland Altman plots for the estimated GFR and the obtained by ^99mTc-DTPA are shown in Figure 2. Ccr showed the best and Schwartz the poorest accuracy, respectively. The predictive performance was evaluated by Sheiner and Beal method, calculating bias as mean prediction error (MPE) and precision (Mean Squared Error, MSE), depicted in Table 3, Ccr had low bias but is unprecise (MPE 1.7, MSE 132) and Schwartz formula the more biased and unprecise (MPE 14.8, MSE 9223), from the equations, the Morris formula was the more unbiased and precise (MPE , MSE 1656).

Figure 1. Correlation Between ^99mTC DTPA and A) Ccr, B) Schwartz Formula, C) Counahan Barrat, D) Morris and E) Leger equations.

Figure 2.Bland-Altman plots for the GFR estimated by Ccr and four equations (n=42). A) Ccr, B) Schwartz, C) Morris and D) Leger equation. The center line corresponds to mean level of bias, the dotted lines depict the upper and lower 95% limits of agreement.

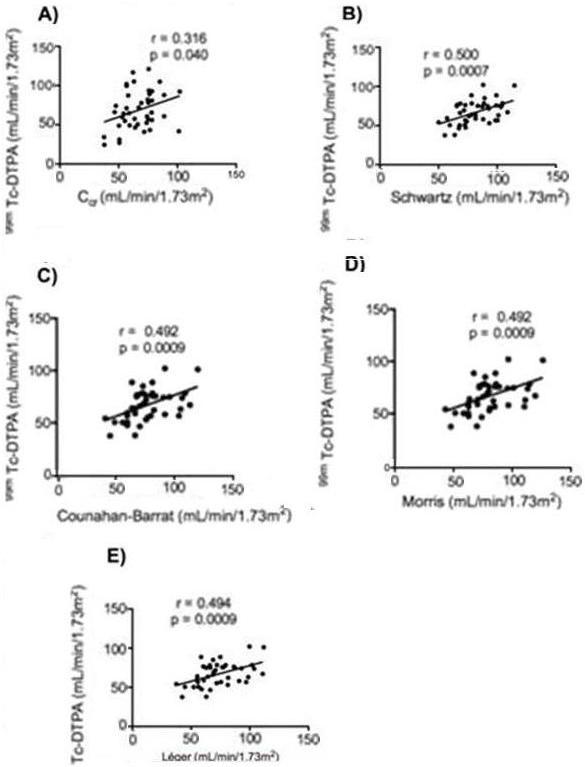
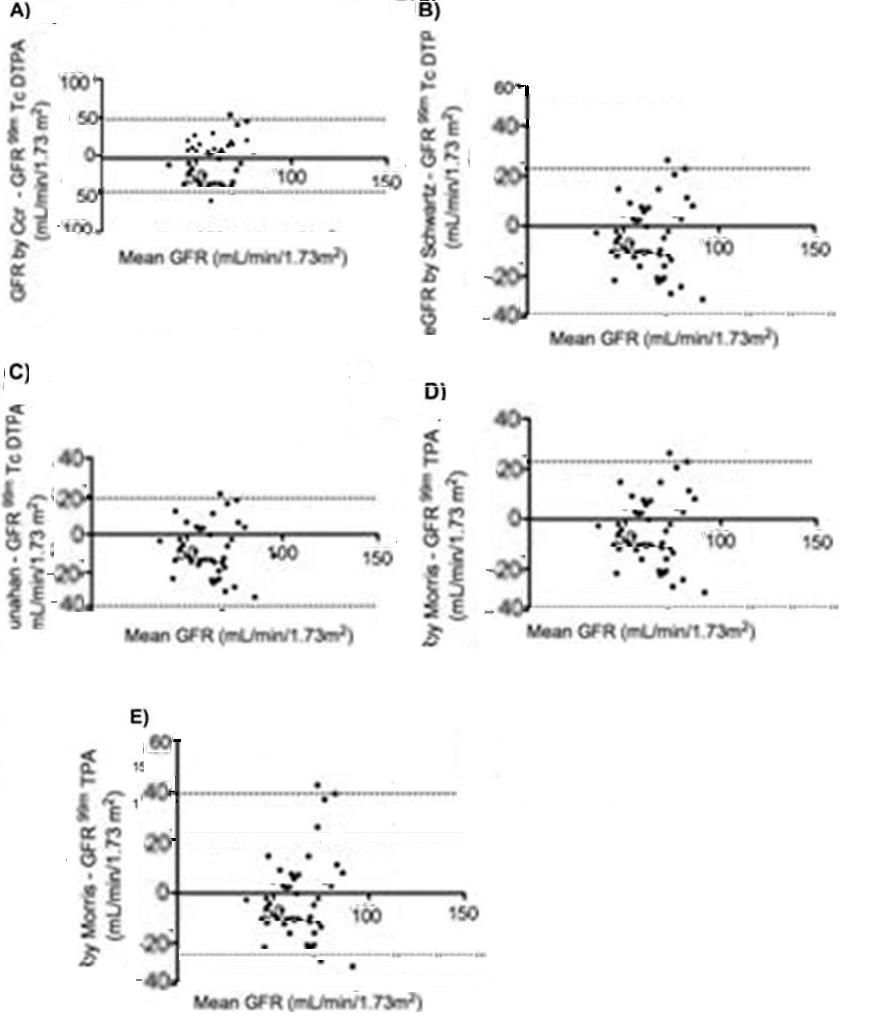
Table 3. Predictive performance of Ccr and four equations to estimate GFR in 42 renal transplant children

	Ccr	Schwartz	Counahan-Barrat	Morris	Leger
MPE	1.73	14.81	-9.40	-6.28	-6.27
MSE	132	9223	3727	1656	2000

MPE: Mean prediction error, MSE: Mean squared error.

Discussion

The equations used to estimate GFR in pediatric patients have an imprecision as high as ± 30-40%, higher than the ± 20% reported in adults [17]. There are few studies evaluating this issue in the context of renal transplant. In adults, the MDRD formula is preferred than the Cockcroft-Gault equation to be used in transplant recipients, nevertheless it is not precise [4, 18] and it can underestimate the patients with declining graft function [8]. The Schwartz formula is the most extensively used to estimate GFR in large pediatric studies such as NAPRTCS and has proven to be a valid outcome variable to measure post-transplant graft function [19, 20]. Zapitelli and coworkers evaluated the Schwartz and the Leger equations to predict iothalamate GFR in 195 children, they found that Schwartz was most unbiased and sensitive [21]. However, in the subset of transplant recipients the Leger had a better performance; the authors attribute this findings to the fact that 42% of the Leger study patients were kidney recipients, they also propose as Van Rossum et al [22] to use locally derived values of k.

More often than not, children receive adult-sized kidneys, Naesens et al [23] demonstrated that when those large kidneys are transplanted into the smallest recipients show a high degree of interstitial fibrosis, tubular atrophy and tubular microcalcifications very early after transplantation. Beside, small children receiving an adult sized kidney have absolute GFR early after transplantation that is similar to the normal GFR that would be expected if they had 2 native kidneys. However, the absolute GFR would not increase as expected, with the growth of the child. This may be due to the non-immunological injury caused by the renal ischemia occurring immediately after transplant, conditioned by the donor-recipient size mismatch. Therefore, the GFR estimated by any method, if normal, may not reflect the real fitness of the graft.

In our study Ccr showed the lowest bias and the higher precision to estimate GFR in renal transplant children. This method is inconvenient as it is cumbersome to patients and their families, and patients without bladder control will require bladder catheterization. Nevertheless, it was the only method found to be not significantly different when evaluated by paired t test, and certainly the cost is lower than the gammagram. Other studies have found a large margin of error in the Ccr since it overestimates the GFR in patients with reduced glomerular function [24], but this was not the case in our study, perhaps due to the fact that our patients were older than 9 years (mean 14.7 years) thus, meaning a better compliance in urine collection. The Morris equation had better predictive performance in renal transplant children than the Schwartz, Counahan-Barrat and Leger equations.

It is necessary to perform further long term comparative studies to determine which one of this methods to estimate GFR is the best to identify children with declining function of the graft.

Acknowledgement

This work was supported by the Fondo Sectorial de Investigacion en Salud 2004- C01-193.

Compliance with Ethical Standards

Funding None

Conflict of Interest None

References

Hogg RJ, Furth S, Lemley KV, Portman R, Schwartz GJ, Coresh J, et al. National Kidney Foundation's Kidney Disease Outcomes Quality Initiative clinical practice guidelines for chronic kidney disease in children and adolescents: evaluation, classification, and stratification. Pediatrics 2003; 111: 1416-1421. [CrossRef]
Filler G, Lepage N. Should the Schwartz formula for estimation of GFR be replaced by cystatin C formula? Pediatr Nephrol 2003; 18: 981-985. [CrossRef]
Seikaly MG, Browne R, Bajaj G, Arant BS, Jr. Limitations to body length/serum creatinine ratio as an estimate of glomerular filtration in children. Pediatr Nephrol 1996; 10: 709-711. [CrossRef]
Mariat C, Alamartine E, Afiani A, Thibaudin L, Laurent B, Berthoux P, et al. Predicting glomerular filtration rate in kidney transplantation: are the K/DOQI guidelines applicable? Am J Transplant 2005; 5: 2698-2703. [CrossRef]
Poge U, Gerhardt T, Palmedo H, Klehr HU, Sauerbruch T, Woitas RP. MDRD equations for estimation of GFR in renal transplant recipients. Am J Transplant 2005; 5: 1306-1311. [CrossRef]
Poge U, Gerhardt T, Woitas RP. Calculation of glomerular filtration rate using serum cystatin C in kidney transplant recipients. Kidney Int 2006; 70: 1878; author reply 1878-1879.
Perico N, Gaspari F, Remuzzi G. Assessing renal function by GFR prediction equations in kidney transplantation. Am J Transplant 2005; 5: 1175-1176. [CrossRef]
Gera M, Slezak JM, Rule AD, Larson TS, Stegall MD, Cosio FG. Assessment of changes in kidney allograft function using creatinine-based estimates of glomerular filtration rate. Am J Transplant 2007; 7: 880-887. [CrossRef]
Hellerstein S, Berenbom M, Erwin P, Wilson N, DiMaggio S. Timed-urine collections for renal clearance studies. Pediatr Nephrol 2006; 21: 96-101. [CrossRef]
Schwartz GJ, Brion LP, Spitzer A. The use of plasma creatinine concentration for estimating glomerular filtration rate in infants, children, and adolescents. Pediatr Clin North Am 1987; 34: 571-590. [CrossRef]
Schwartz GJ, Furth SL. Glomerular filtration rate measurement and estimation in chronic kidney disease. Pediatr Nephrol 2007; 22: 1839-1848. [CrossRef]
Schwartz GJ, Haycock GB, Spitzer A. Plasma creatinine and urea concentration in children: normal values for age and sex. J Pediatr 1976; 88: 828-830. [CrossRef]
Counahan R, Chantler C, Ghazali S, Kirkwood B, Rose F, Barratt TM. Estimation of glomerular filtration rate from plasma creatinine concentration in children. Arch Dis Child 1976; 51: 875-878. [CrossRef]
Morris MC, Allanby CW, Toseland P, Haycock GB, Chantler C. Evaluation of a height/plasma creatinine formula in the measurement of glomerular filtration rate. Arch Dis Child 1982; 57: 611-615. [CrossRef]
Leger F, Bouissou F, Coulais Y, Tafani M, Chatelut E. Estimation of glomerular filtration rate in children. Pediatr Nephrol 2002; 17: 903-907. [CrossRef]
Sheiner LB, Beal SL. Some suggestions for measuring predictive performance. J Pharmacokinet Biopharm 1981; 9: 503-512. [CrossRef]
Gretz N, Schock D, Sadick M, Pill J. Bias and precision of estimated glomerular filtration rate in children. Pediatr Nephrol 2007; 22: 167-169. [CrossRef]
Gaspari F, Ferrari S, Stucchi N, Centemeri E, Carrara F, Pellegrino M, et al. Performance of different prediction equations for estimating renal function in kidney transplantation. Am J Transplant 2004; 4: 1826-1835. [CrossRef]
Sorof JM, Goldstein SL, Brewer ED, Steiger HM, Portman RJ. Serial estimation of glomerular filtration rate in children after renal transplant. Pediatr Nephrol 1999; 13: 737-741. [CrossRef]
Ellis EN, Martz K, Talley L, Ilyas M, Pennington KL, Blaszak RT. Factors related to long-term renal transplant function in children. Pediatr Nephrol 2008;23 : 1149-1155. [CrossRef]
Zappitelli M, Joseph L, Gupta IR, Bell L, Paradis G. Validation of child serum creatinine-based prediction equations for glomerular filtration rate. Pediatr Nephrol 2007; 22: 272-281. [CrossRef]
Van Rossum LK, Mathot RA, Cransberg K, Zietse R, Vulto AG. Estimation of the glomerular filtration rate in children: which algorithm should be used? Pediatr Nephrol 2005; 20: 1769-1775. [CrossRef]
Naesens M, Kambham N, Concepcion W, Salvatierra O, Jr., Sarwal M. The evolution of nonimmune histological injury and its clinical relevance in adult-sized kidney grafts in pediatric recipients. Am J Transplant 2007; 7: 2504-2514. [CrossRef]

Cite this article as:

Ulibarri B, Martinez-Duncker C, Camarillo C, Guadarrama E O, Roca P G, Arizpe R M, Medeiros M. Comparison of 99m Tc DTPA vs Five Methods to Estimate Glomerular Filtration Rate in Children with Renal Transplantation. Pediatr Oncall J. 2009;6: 67-70.

Home

Articles & Issues

About

Contribute

Pediatric Oncall Journal

Comparison of 99m Tc DTPA Vs Five Methods To Estimate Glomerular Filtration Rate In Children With Renal Transplantation.

Home

Partner Sites